残局

不过在等杀死希望的最后一刀

0%

红黑树

发表于 更新于
本文字数： 4.2k 阅读时长 ≈ 4 分钟

引入

由于二叉搜索树很不平衡，很容易退化为一条类似链表的结构，从而造成时间复杂度从$O(lgN)$降低为$O(N)$。

为解决这一问题，引入了“平衡”二叉搜索树，红黑树就是其中的一种。红黑树在树的基础上，为每个节点增加了一个颜色位，可以是RED，也可以是BLACK。通过对每条路径的颜色进行约束，保证红黑树处于近似平衡的状态，从而保证了查找最坏情况为$O(lgN)$。

特性

红黑树除了本身是二叉搜索树外，还满足以下条件：

  1. 每个节点要么是红色的，要么是黑色的。
  2. 根节点是黑色的。
  3. 每个空节点(NIL)都是黑色的。
  4. 红色节点的两个子节点都是黑色的。
  5. 每个节点到其后代叶子节点的路径上包含的黑色节点数目相同。

红黑树的定义如下：

1
2
3
4
5
6
7
8
9
10
11
enum RBTColor{RED, BLACK};

template <class T>
class RBTNode{
    public:
    	T key;
        RBTColor color;
        RBTNode *left;
        RBTNode *right;
        RBTNode *parent;
};

样例如图：

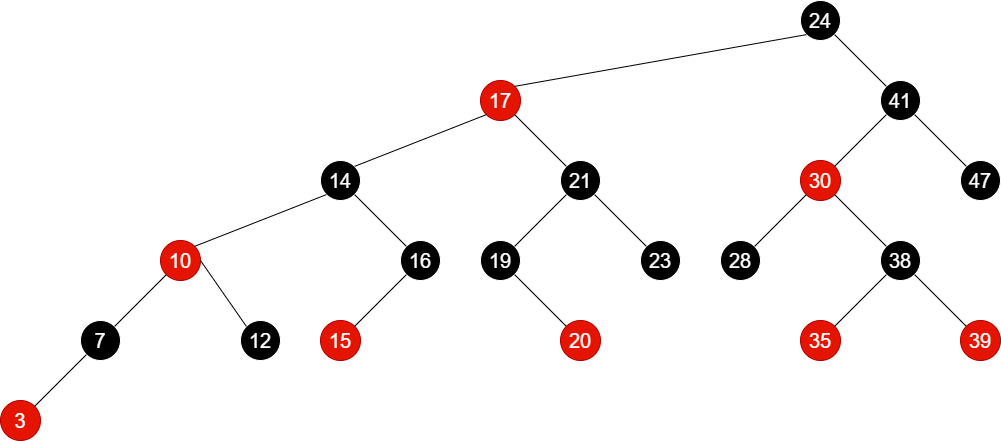
红黑树样例

算法

旋转

由于结点的插入、删除操作对树进行了修改。修改后的红黑树可能不再满足上面所列出的红黑性质，故需要对树的某些结点进行旋转或变色使其自平衡。

忽略红黑特性，以一个二叉搜索树为例进行演示旋转。样例如下：

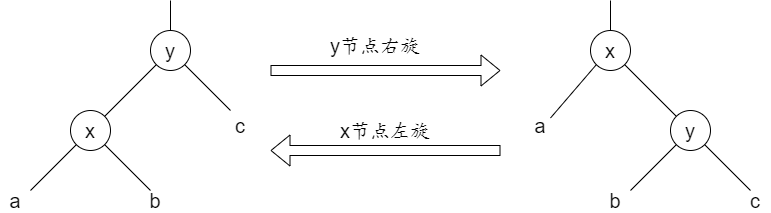
红黑树旋转

图中x y是两个节点，a b c表示任意子树。

不难看出，图中的旋转仍然保持了二叉搜索树的性质：a子树所有节点的key值小于x.key;c子树所有节点的key值大于y.key;b子树key值介于x.key与y.key之间。伪代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
//左旋
LEFT-ROTATE(T, x)
y = x.right					
x.right = y.left			//上图中，b子树的移动
if y.left != nullptr
    y.left.parent = x		//过继过去的b子树父节点改变
y.parent = x.parent
    //改变x的父节点的指向
if x.parent == nullptr
    T.root = y				//x父节点为空，证明x为根节点 即左旋后的y节点变为根节点
else if x == x.parent.left
    x.parent.left = x
else
    x.parent.right = y
y.left = x					//将x链接在y的左侧
x.parent = y

//右旋
RIGHT-ROTATE(T, y)
x = y.left
y.left = x.right
if x.right != nullptr
    x.right.parent = y
x.parent = y.parent
if y.parent == nullptr
    T.root = x
else if y == y.parent.left
    y.parent.left = x
else
    y.parent.right = x
x.right = y
y.parent = x

旋转操作只改变所旋转元素附近的指针，其他属性均未改变。可以在常数时间$O(1)$内完成。

插入

由于红黑树对黑色节点的要求较为苛刻，新插入的节点默认为红色。

将某个节点插入到红黑树，详细过程如下：

  1. 首先，红黑树本身是一个二叉搜索树，依据其性质可以找到相应的插入位置，保证节点插入后key仍有序。
  2. 插入后，进行一系列的旋转、着色使其继续保持红黑特性。

正常情况下(排除红黑树从0开始构建的情况)，当我们插入一个节点后如果违反了红黑树的红黑特性，那么所违反的应该为特性4(红节点的两个子节点均为黑色)。我们需要从当前节点向根节点逐层向上判断是否调整并作出相应的调整。相关调整方案如下：

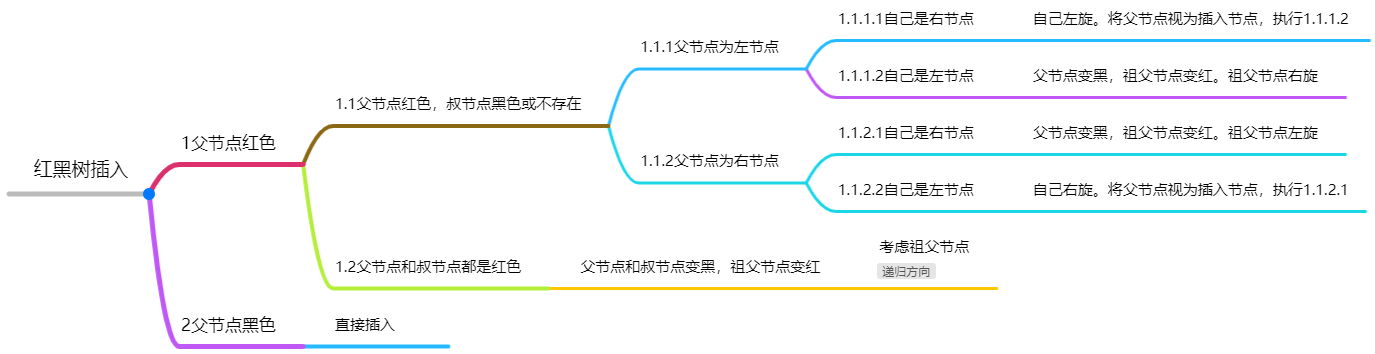
RBTreeInsert

最后，根节点恒染为黑色。

下面给出一个范例，显示一个红黑树上的调整操作。

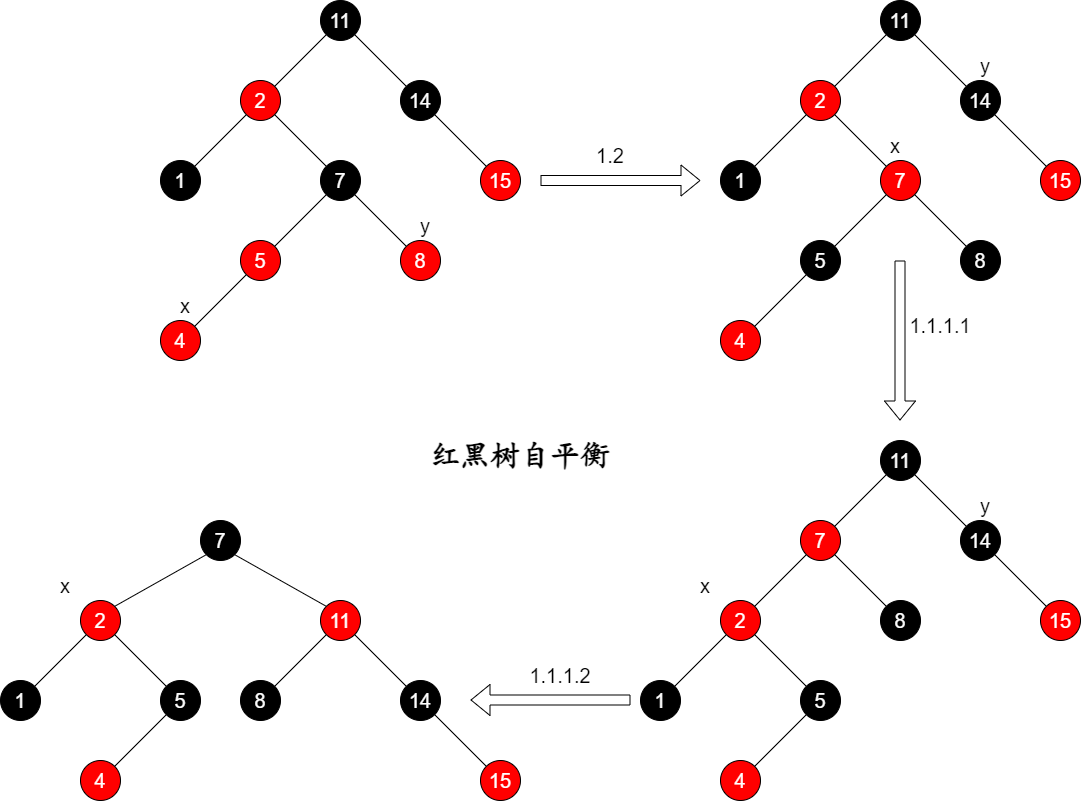
RBTreeInsertExp

在上图中，初始状态x为插入的节点，其父节点(key = 5)违背红黑规则4，需要进行调整：

  1. 由于x的父节点和叔节点都是红色（调整方案1.2），调整时需要将其父节点(key = 5)和叔节点(key = 8)染成黑色，将其祖父节点(key = 7)染成红色，然后考虑其祖父节点。x节点上移为其祖父节点(key = 7)，此时x节点的父节点(key = 2)违背红黑规则4
  2. 叔节点不为红色，调整策略对应为1.1。观察到父节点是祖父节点的左子树，自己是父节点的右节点(1.1.1.1)。当前节点上移为其父节点(key = 2)然后左旋。左旋后的x节点执行调整方案1.1.1.2
  3. 父节点(key = 7)染成黑色，祖父节点(key = 11)染成红色，将祖父节点右旋。x节点的父节点(key = 11)不再是红色，退出循环。此时当前红黑树不再违背红黑规则。
  4. 循环退出后，将其根节点染成黑色。

调整方案对应的伪代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
while x.parent.color == RED		// 1
    if x.parent == x.parent.parent.left
        y = x.parent.parent.right	//叔节点
        if y.color == RED		//1.2
            x.parent.color = BLACK
            y.color = BLACK
            x.parent.parent.color = RED
            x = x.parent.parent
        else
            if x == x.parent.right	//1.1.1.1
                //父节点左旋并置为当前
                x = x.parent
                LEFT-ROTATE(T, x)
            //1.1.1.2
            x.parent.color = BLACK
            x.parent.parent.color = RED
            RIGHT-ROTATE(T, x.parent.parent)
    //父节点为右
    else
        y = x.parent.parent.left
        if y.color == RED
            x.parent.color = BLACK
            y.color = BLACK
            x.parent.parent.color = RED
            x = x.parent.parent
        else
            if x == x.parent.left //1.1.2.2
                x = x.parent
                RIGHT-ROTATE(T, x)
            //1.1.2.1
            x.parent.color = BLACK
            x.parent.parent.color = RED
            LEFT-ROTATE(T, x.parent.parent)
T.root.color = BLACK

删除

删除和插入操作类似，也分为两个步骤：

  1. 红黑树本身是一个二叉搜索树，根据其性质寻找到对应节点并删除掉。删除的情况如下
    • 若该节点是叶子节点，则直接删除。
    • 若只有一个子树，则用子树替代当前节点。
    • 若有两个子树，则用右子树的最小值(大于被删除元素的最小值)替代当前节点。
  2. 通过旋转、着色等操作将红黑树修正，使之成为新的红黑树。

根据所替代节点的相关信息来进行调整：

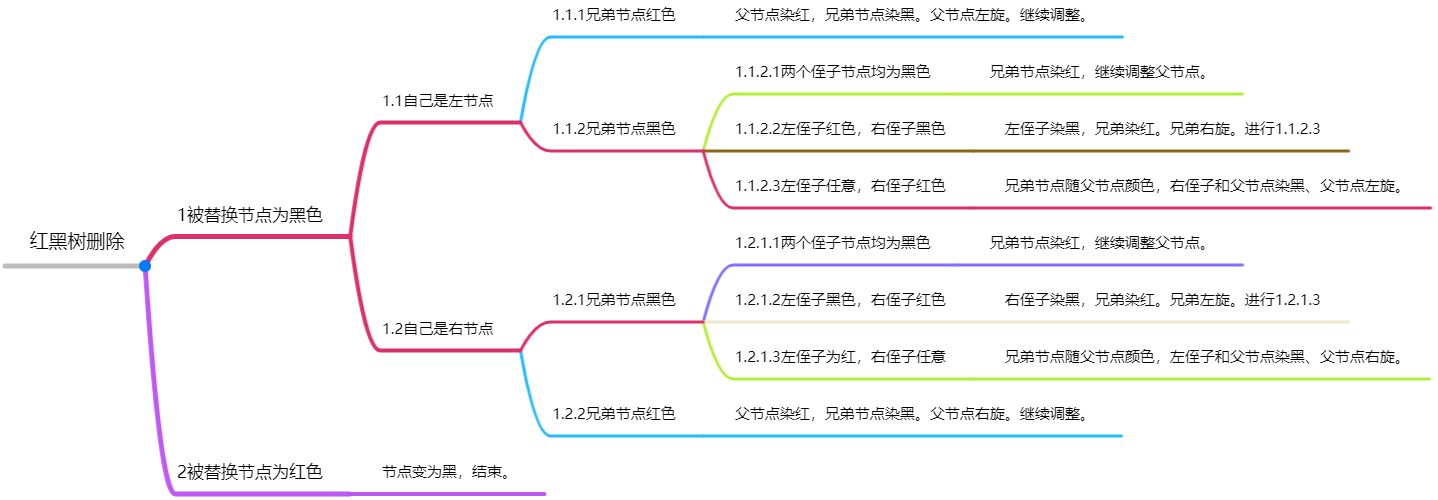
RBTreeDelete

同样的，在循环结束之后，将当前节点染成黑色。

下面给出几个具体样例进行分析：

  • 例一

    RBTreeDeleteExp1

    在该样例中，A节点为黑色，且是其父节点的左节点，兄弟节点D为红色，满足调整方案1.1.1。所做出的调整为将其父节点B染成红色，兄弟节点D染成黑色。然后将其父节点B进行左旋。此后均满足条件。

  • 例二

    RBTreeDeleteExp2

    在该样例中，A节点为黑色，且是其父节点的左节点，兄弟节点D为黑色，两个侄子节点C和E均为黑色，满足调整方案1.1.2.1。调整时，将其兄弟结点D染成红色，x已上移为根节点B，循环结束。需要特别注意的是，此刻应再将节点B染成黑色。

  • 例三

    RBTreeDeleteExp3

    在该样例中，A节点为黑色，且是其父节点的左节点，兄弟节点D为黑色，左侄子C为红色,右侄子E为黑色，满足调整方案1.1.2.2。调整时，将其左侄子C染成黑色，兄弟节点D染成红色，并将兄弟节点D右旋，然后再按照调整方案1.1.2.3进行调整，在此略过。

  • 例四

    RBTreeDeleteExp4

    在该样例中，A节点为黑色，且是其父节点的左节点，兄弟节点D为黑色，右侄子E为红色，满足调整方案1.1.2.3。调整时，兄弟节点D颜色随父节点B，右侄子E和父节点B染成黑色，将父节点B左旋。

调整方案对应伪代码如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
while x != T.root and x.color == BLACK
    if x == x.parent.left
		w = x.parent.right			//兄弟节点
        if w.color == RED			// 1.1.1
            w.color = BLACK
            x.parent.color = RED
            LEFT-ROTATE(T, x.parent)
            w = x.parent.right
        if w.left.color == BLACK and w.right.color == BLACK		//1.1.2.1
            w.color = RED
            x = x.parent
        else
            if w.right.color == BLACK						//1.1.2.2
            	w.left.color = BLACK
                w.color = RED
                RIGHT-ROTATE(T, w)
               	w = x.parent.right
            w.color = x.parent.color	//1.1.2.3
            x.parent.color = BLACK
            w.right.color = BLACK
            LEFT-ROTATE(T, x.parent)
            x = T.root
    else
        w = x.parent.left
        if w.color == RED		//1.2.2
            w.color = BLACK
            x.parent.color = RED
            RIGHT-ROTATE(T, x.parent)
            w = x.parent.left
        if w.right.color == BLACK and w.left.color == BLACK	//1.2.1.1
            w.color =RED
            x = x.parent
        else
            if w.left.color == BLACK	//1.2.1.2
                w.right.color = BLACK
                w.color = RED
                LEFT-ROTATE(T, w)
            w.color = x.parent.color	//1.2.1.3
            x.parent.color = BLACK
            w.left.color = BLACK
		   RIGHT-ROTATE(T, x.parent)
            x = T.root
x.color = BLACK

后记

红黑树插入、删除节点的情况虽然复杂，但基本处于对称情况，且有一个模型通过拼凑其他模型来实现。本文中的伪代码、样例均选自《算法导论》，红黑树的图采用drawio绘制。

-------------感谢阅读有缘再见-------------