左孩子右兄弟表示法

对于任意一个结点T，其仅包含两个指针：

T.left-child，指向T结点的最左侧子节点。
T.right-sibling，指向T右侧最邻近的兄弟结点。

特别的，当二者不存在时，相应的指针皆为空，即NIL。该方法只需要 $O (n)$ 空间来存储含 $n$ 个结点的树。

由于其与二叉树的相似性，故又叫树的二叉树表示法。

在此，给出一个样例：

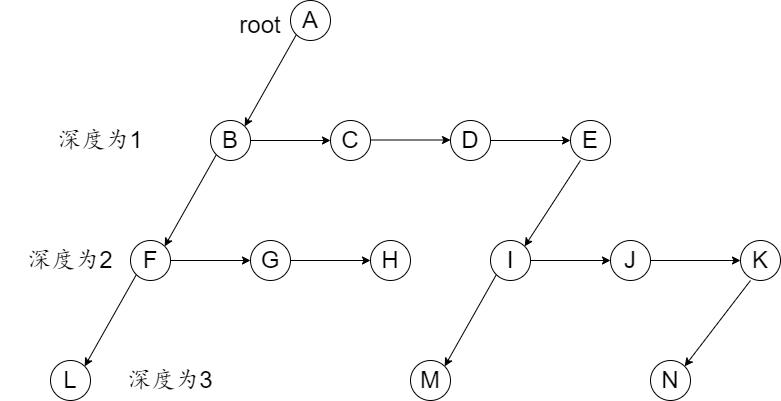
该样例旨在为下述算法提供一个参考。

相关算法

深度

对于该种树而言，任意一个节点和其右节点的深度相同。也就意味着对于一个节点T，其高度为要么和右子树高度相同，要么比左子树低一层。从叶子节点向上递归，即可得出最大深度。即：

int Height(Tree& t){
	if(t == nullptr) return 0;
	return Height(t->left) + 1 > Height(t->right) ? Height(t->left) + 1 : Height(t->right);
} 

叶子节点数

基于二叉树中的定义，叶子节点是没有子节点的节点。在该种表示方法中，即左指针为空的节点（某一层的最后一个叶子节点右子树也为空，故只看左指针就行）。对于一个节点的叶子节点数，即：

int Count(Tree& t){
	if(t == nullptr) return 0;
	if(t->left == nullptr) return 1;
	return Count(t->left) + Count(t->right); 
}

遍历

先序遍历

先序遍历，对于某个节点而言，其左指针为第一个子节点。向左指针递归即寻找孩子，回溯时输出右指针的兄弟。与二叉树的先序遍历完全一致。

void preOrder(Tree& t){
	if(t == nullptr) return;
	cout<<t->val<<" ";	//输出值
	TreeNode* p = t->left;
	while(p != nullptr){
		preOrder(p);
		p = p->right;
	}	
}

后序遍历

后序遍历过程中，对于一个节点，应该打印其左指针和全部右侧的节点后才打印该节点，即回溯时才打印当前节点。

void PostOrder(Tree& t){
	if(t == nullptr) return;
	TreeNode* p = t->left;
	while(p != nullptr){
		PostOrder(p); 	//递归找“根”
		p = p->right;
	}
	cout<<t->val<<" ";
} 

层序遍历

层序遍历，即类似于广度优先算法。对于一个节点，当打印左节点时，应将其右侧所有兄弟节点都打印再去下一层。打印其兄弟节点时，保留其左节点，即其子节点的兄弟。基于此，也可统计出每层的宽度。有注释的几行即为相应的宽度统计。

void levelOrder(Tree& t){
	if(t == nullptr) return;
	queue<TreeNode*> q;
	TreeNode* p;
    int max = INT_MIN; //宽度
	q.push(t);
	while(!q.empty()){
		int width = q.size();		
		for(int i = 0;i < width;i ++){
			p = q.front();
			q.pop();
			cout<<p->val<<" ";
			p = p->left;
			while(p != nullptr){
				q.push(p);
				p = p->right;
			}
		}
        max = max > width ? max: width;        //一层遍历结束 统计宽度
		cout<<endl;
	}
    return max;			//返回宽度
}

残局

左孩子右兄弟树