AVL 树和红黑树都假设所有的数据放在主存当中。而当数据量达到亿级,主存中根本存储不下,我们只能以块的形式从磁盘读取数据,与主存的访问时间相比,磁盘的 I/O 操作相当耗时,而提出 B-树的主要目的就是减少磁盘的 I/O 操作。
B树的一个节点
性质
B树所具有的的性质人如下:
- 每个节点
- 节点
- 每个非叶子节点还包括
4. 所有的叶子节点深度相同
5. B树的最小度数
1. 除根节点外,每个节点必须至少有
2. 每个节点至多有
一个B树的样例如下:
一个较为简单的B树定义
1 | class BTreeNode |
B树的高度
B树大部分操作的磁盘存取次数与B树的高度成正比。对于任意一个包含
基本操作
在此假定:B树始终在主存中,无需读取磁盘。
搜索
B树的搜索,不过是在二叉搜索树的基础上,每个节点有多个
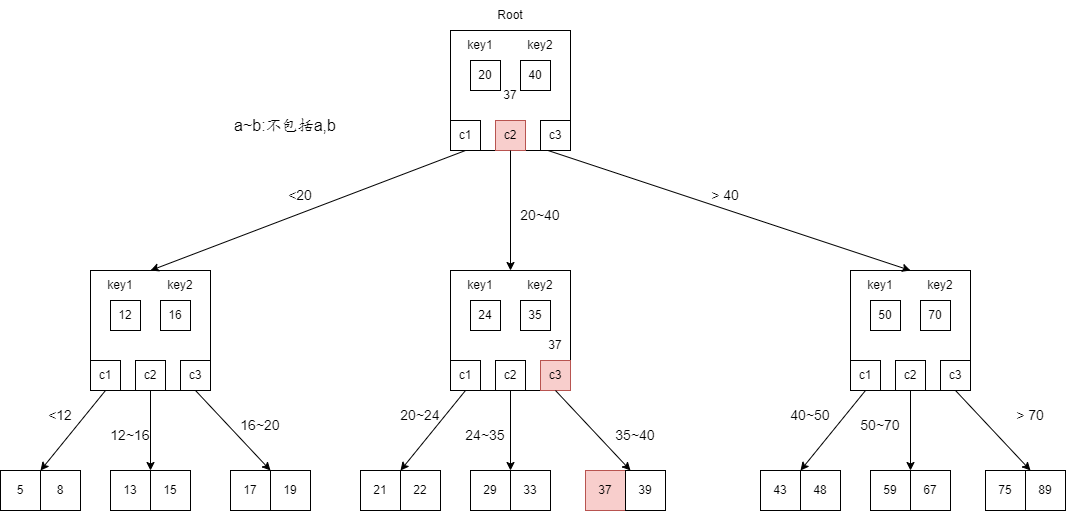
以上述的样例图中查找33为例。
- 首先,访问根节点。先和第一个

- 接着,访问

- 最后在叶子节点
相关过程代码如下:插入、删除。过于复杂,先略了,有空再写。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18BTreeNode *BTreeNode::search(int k)
{
// 找到第一个大于待查找k 的key值
int i = 0;
while (i < n && k > keys[i]) {
i++;
}
// 相等即找到
if (keys[i] == k)
return this;
// 如果没有找到,且当前结点为叶子结点则无解
if (leaf == true)
return nullptr;
// 递归访问恰当的子代
return C[i]->search(k);
}