残局

不过在等杀死希望的最后一刀

0%

STL源码-容器

发表于 更新于
本文字数： 25k 阅读时长 ≈ 23 分钟

本文是在阅读SGI STL v3.3源码中关于container部分，遇到的一些问题及有意思的点。

此外，本文建立在已经观看过侯捷老师STL源码剖析课程的基础上。是在阅读源码过程中，对其中的内容进行补充、修饰。

顺序型容器

vector

#pragma set woff XXX

  • #pragma set woff xxx —- 关闭/抑制 名为xxx的编译器警告
  • #pragma reset woff xxx —- 重置命令行中指定的状态的警告（取消set状态）

static_assert

C++11 静态断言static_assert，编译期断言。

static_assert(常量表达式，提示信息)

与断言的区别是，静态断言如果为假，则编译不通过。

noexcept

noexcept 是C++11中的特性，既是一个说明符，也是一个运算符。noexcept指示函数不会抛出异常，编译器可以优化代码。

noexcept 用法：

  1. return_type function() noexcept不会抛出异常
  2. return_type function() noexcept(常量表达式)常量表达式为true，则不会抛出异常。

使用场景：移动构造函数、移动赋值、swap()、析构函数。

  • ==默认==的构造函数、拷贝构造函数、赋值、移动构造、移动赋值均为noexcept。
  • c++11仍保留throw()，实现和noexcept类似功能（但throw不会针对编译器优化），但在c++20已删除。

explicit

explicit关键字用于构造函数之前，默认关闭了隐式类型转换。

通过构造函数将相应的数据类型转换成为C++类的对象，给编码带来了方便，但并不是每次都正确，为了避免这种情况引入explicit。

explicit 关键字只能用于修饰只有一个参数的类构造函数

const_iterator

const_iterator可以改变iterator的值，但不能通过iterator修改指向元素内容的值。(指向常量的指针)

max_size()

max_size()函数如下：

1
2
size_type max_size() const
  { return size_type(-1) / sizeof(_Tp); }

由源码可以知道，size_type为无符号整形。而-1我们知道其二进制补码为==全1==。size_type(-1)将其强制类型转换为无符号整形的最大值(==全1==)，即表示最大值232/64。然后对应的除以一个元素所占大小，即得出最大存放元素数量。

根据操作系统的位数自由推断所能存储的最大元素数量。

copy()

这里所写的copy(iter it1,iter it2,iter it3)函数是将vector的拷贝赋值=，目的地址所存在的元素数多于要插入的元素时的状况：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
vector<_Tp,_Alloc>::operator=(const vector<_Tp, _Alloc>& __x)
{
  if (&__x != this) {
    const size_type __xlen = __x.size();
    if (__xlen > capacity()) {
        ......
    }
    else if (size() >= __xlen) {
      iterator __i = copy(__x.begin(), __x.end(), begin());
      destroy(__i, _M_finish);
    }
    else {
        ......
    }
    _M_finish = _M_start + __xlen;
  }
  return *this;
}

该copy()函数最终调用的函数如下:

1
2
3
4
5
6
template <class _Tp>
inline _Tp*
__copy_trivial(const _Tp* __first, const _Tp* __last, _Tp* __result) {
  memmove(__result, __first, sizeof(_Tp) * (__last - __first));
  return __result + (__last - __first);
}

construct()

该函数存在于stl_construct头文件中，是分配器的一部分。源码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
template <class _T1, class _T2>
inline void construct(_T1* __p, const _T2& __value) {
  _Construct(__p, __value);
}

template <class _T1>
inline void construct(_T1* __p) {
  _Construct(__p);
}

template <class _T1, class _T2>
inline void _Construct(_T1* __p, const _T2& __value) {
  new ((void*) __p) _T1(__value);   // placement new，调用 _T1::_T1(__value);
}

template <class _T1>
inline void _Construct(_T1* __p) {
  new ((void*) __p) _T1();
}
  • __p —- 指针
  • __value —- 初值
  • 函数功能 —- 将初值 __value 设定到指针__p所指的空间上

函数的作用在于调用相应的构造函数，将地址进行类型转换。

copy_backward()

copy_backward(iter1 first,iter1 end, iter2 res)将元素[first,end)复制到以res为尾迭代器的位置[res−(end−first),res)。（当在中间插入元素时，后续部分移动copy_backward(*__position*, _M_finish - 2, _M_finish - 1);）样例：

1
2
3
4
5
vector<int>v1{1,2,3,4,5};
copy_backward(v1.begin()+1,v1.begin()+3,v1.end());//1~3号元素的值赋给x~_finish。
for(auto iter=v1.begin();iter!=v1.end();++iter){
    cout<<*iter<<" ";
}	//1 2 3 2 3

bit_vector

由于bool类型只用1bit就可以表示，不需要1Bytes，因此对vector提供相应的偏特化版本。虽然一个元素只占1bit，但地址空间是按照unsigned int进行分配。

我们知道，vector由start,finish,end_of_storage三个迭代器组成，大小为12字节。而bit_vector与vector存在着一定的差异：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
//与大小无关的代码已省略
class _Bvector_base
{
  _Bit_iterator _M_start;
  _Bit_iterator _M_finish;
  unsigned int* _M_end_of_storage;  
};
struct _Bit_iterator : public _Bit_iterator_base
{
...
};
struct _Bit_iterator_base : public random_access_iterator<bool, ptrdiff_t> 
{
  unsigned int* _M_p;	//指向具体实体
  unsigned int _M_offset;	//偏移量(从0开始 用于找到具体bit位)
};

struct _Bit_reference {
  unsigned int* _M_p;	//指向具体实体
  unsigned int _M_mask;	//vaule(true or false)
};
  • __WORD_BIT —- 由于不同位数的操作系统下unsigned int大小并不固定，因此用来确认具体大小。

可以看出，每个bit_vector由一个unsigned int*和两个iterator组成，而一个bit_iterator由unsigned int*和unsigned int组成，占大小20Bytes

与bit_iterator相关联的两个函数_M_bump_down和_M_bump_up用来进行移位。基于这两个函数还重写了++ --运算符

flip()

所有元素取反。(true->false,false->true)

list

begin()/end()

双向链表底层存放的是虚拟头部(_M_head)，begin()函数返回的是_M_head->_M_next。而双向链表涉及的是==循环==结构，尾结点的next指针指向虚拟头部。end()函数返回尾结点的下一个元素，即_M_head。

transfer()

list中存在一个transfer(iter postion,iter first,iter last)函数。用于将[first,last)元素移动到position之前。

源码如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void transfer(iterator __position, iterator __first, iterator __last) {
  if (__position != __last) {
    // Remove [first, last) from its old position.
      //改正序遍历指针
    __last._M_node->_M_prev->_M_next     = __position._M_node;
    __first._M_node->_M_prev->_M_next    = __last._M_node;
    __position._M_node->_M_prev->_M_next = __first._M_node; 

    // Splice [first, last) into its new position.
      //改逆序遍历指针
    _List_node_base* __tmp      = __position._M_node->_M_prev;
    __position._M_node->_M_prev = __last._M_node->_M_prev;
    __last._M_node->_M_prev     = __first._M_node->_M_prev; 
    __first._M_node->_M_prev    = __tmp;
  }
}

以1~7节点中移动[4,6)为例

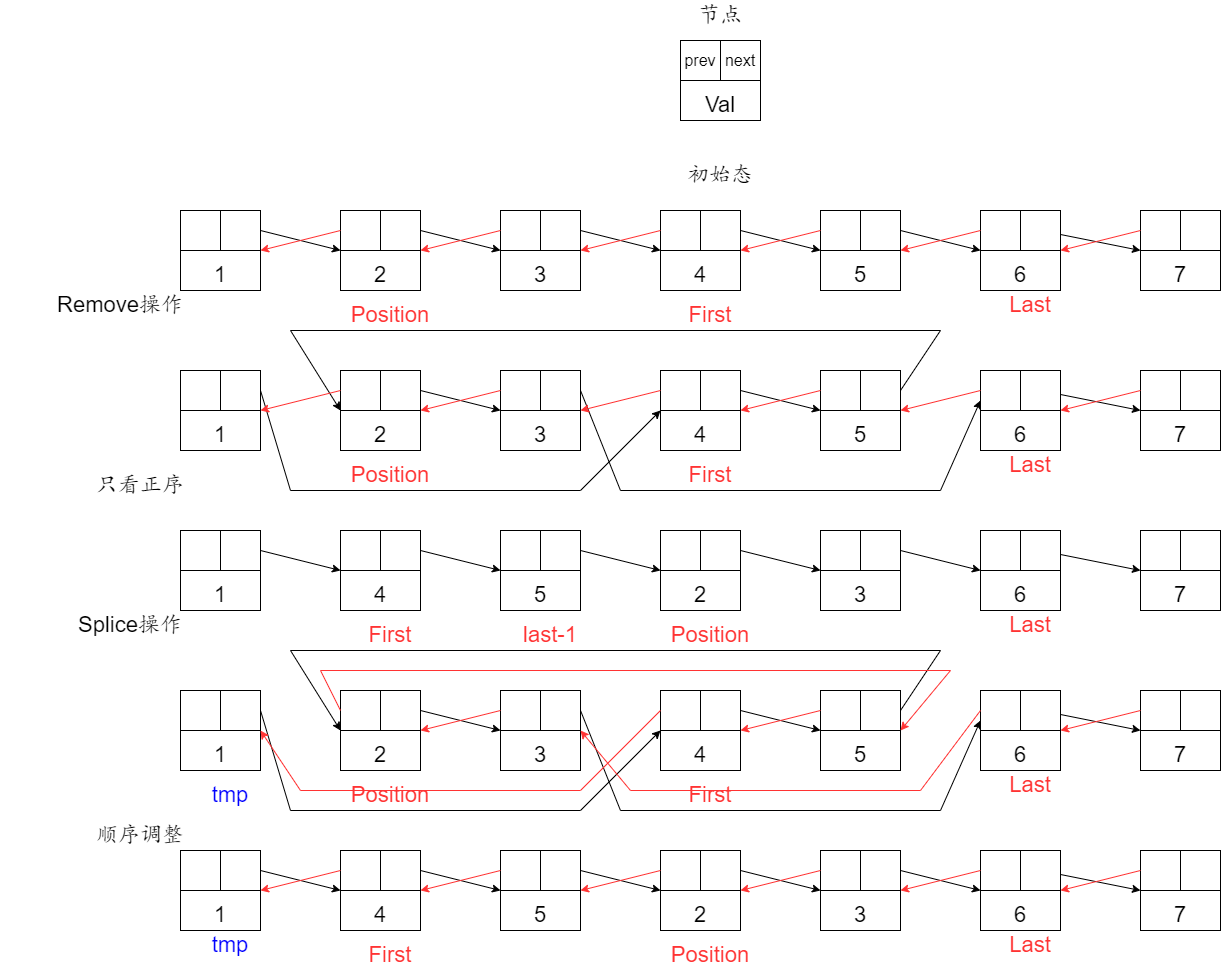
transfer

splice()

splice()底层是调用transfer()，将元素(结点、list、起止迭代器)插入到指定位置(position)之前。

unique()

删除==连续==的相同元素（保证唯一）。

merge()

  • 将另一个链表list2合并到该链表上。

  • 合并有序链表，合并后仍有序。

  • 两个指针分别指向两个链表头。以调用函数的list为基准，比较大小决定list2结点插入的位置。

sort()

list::sort本质上是归并排序。依次从源链表中取值，放入__counter数组中。__counter数组第i层至多存放2i个元素(共可以存放264−1个元素)。在递归过程中，先在第0层插入，然后该层元素满时，向上传递该层的数组，并找到恰当的位置。当一层的元素进入下一层是该层元素构成的数组是有序的，被插入的深层里的元素也是有序的（归并排序）。当所有元素都读取出之后while(!empty())跳出，然后递归遍历，每一层都向上传输并进行归并排序。最终将得到的结果回写给源链表。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
template<class T, class Alloc>
void list<T, Alloc>::sort() {
    if (node->next == node || link_type(node->next)->next == node) return;
    list<T, Alloc> carry;       //辅助链表，相当与tmp
    list<T, Alloc> counter[64]; //保存当前递归层次的结果，第i链表保存的元素个数为2的i次方或0
    int fill = 0;
    while (!empty()) {
        carry.splice(carry.begin(), *this, begin());  //将链表的第一个元素移动至carry开头
        int i = 0;
        //从小到大不断合并非空归并层次直至遇到空层或者到达当前最大归并层次
        while (i < fill && !counter[i].empty()) {
            counter[i].merge(carry);  //合并链表，结果链表是有序的，必须保证合并前两链表有序
            carry.swap(counter[i++]); //链表元素互换
            //将某一层的元素换出到carry中，去和下一层比对
        }
        carry.swap(counter[i]);  //将carry元素放到counter[i]中，相当于将carry情况，带下一次循环使用
        //将carry中的数据换回最深层
        if (i == fill) ++fill;
    }
    //将所有归并层次的结果合并得到最终结果counter[fill-1]
    for (int i = 1; i < fill; ++i) counter[i].merge(counter[i-1]);
    swap(counter[fill-1]);
}
  • fill —- counter数组中最深层的层数

slist

slist、forward_list。单向链表。仅有一个虚拟头部，指向实际链表头

__slist_splice_after()

_Slist_node_base == A

  • __slist_splice_after(A* pos,A* first,A*last)将(first,last]中的数据移动到pos之后
  • __slist_splice_after(A* pos,A* node)将(node,∞)移动到pos之后。（node之后所有元素）

_M_erase_after()

  • _M_erase_after(A* pos)删除pos位置后的第一个元素
  • _M_erase_after(A* pos, A* last)删除(post,last)之间全部元素

begin()/end()

  • 单向链表的底层仅存在一个虚拟头部(_M_head)指向真正链表的头，begin()函数返回的是_M_head->_M_next
  • 由于end()应指向最后一个元素的下一个元素(nullptr)，而单链表只能单向访问，直接return nullptr

push/pop

单链表插入/删除元素是在==头部==进行操作。故，push/pop函数为push_front()/pop_front()，插入/弹出虚拟头部的后一个位置。

previous()

previous(iterator pos)返回pos位置的前一个元素。

deque

结构

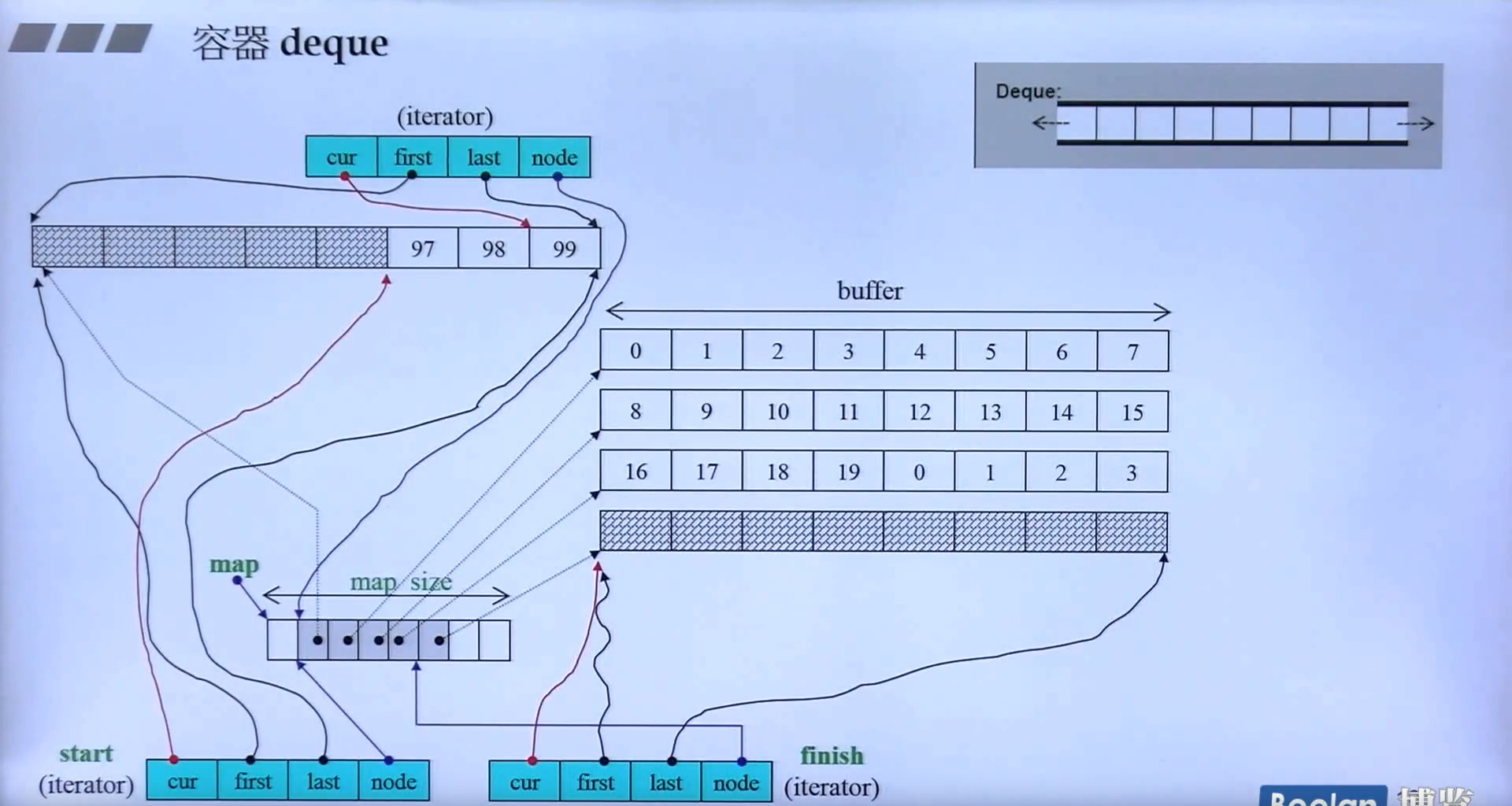
deque

_Deque_iterator
1
2
3
4
5
6
7
8
template <class _Tp, class _Ref, class _Ptr>
struct _Deque_iterator {
    typedef _Tp** _Map_pointer;
  _Tp* _M_cur;   // 迭代器指向缓冲区的当前元素
  _Tp* _M_first; // 迭代器指向缓冲区的头部
  _Tp* _M_last;  // 迭代器指向缓冲区的尾部
  _Map_pointer _M_node;  // 迭代器指向 map 的 node
}

operator-

1
2
3
4
5
6
7
8
difference_type operator-(const self& x) const {
    return difference_type(buffer_size()) *(node - x.node - 1) + (cur - first) + (x.last - x.cur);
    /*
    node - x.node - 1     map中的完整缓冲区个数
    cur - first 尾迭代器buffer元素个数
    x.last - x.cur 头迭代器buffer元素个数
    */
}

enum { _S_initial_map_size = 8 }; //默认map大小

_M_initialize_map()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
template <class _Tp, class _Alloc>
void
_Deque_base<_Tp,_Alloc>::_M_initialize_map(size_t __num_elements)
{
  // 所需节点数
  size_t __num_nodes = 
    __num_elements / __deque_buf_size(sizeof(_Tp)) + 1;
    // __num_elements / __deque_buf_size(sizeof(_Tp))满结点个数 + 1未满（或空）
  // 一个 map 要管理几个节点，最少 8 个，最多是所需节点数加 2（首尾两个虚拟节点）
  _M_map_size = max((size_t) _S_initial_map_size, __num_nodes + 2);
  _M_map = _M_allocate_map(_M_map_size);

  // __nstart、__nfinish 指向 map 的中间位置。方便两端扩充（减少加结点的次数）
  _Tp** __nstart = _M_map + (_M_map_size - __num_nodes) / 2;
  _Tp** __nfinish = __nstart + __num_nodes;
    
  __STL_TRY {
    _M_create_nodes(__nstart, __nfinish);
  }
  __STL_UNWIND((_M_deallocate_map(_M_map, _M_map_size), 
                _M_map = 0, _M_map_size = 0));
  // 为 deque 内的两个迭代器 start 和 finish 指向正确位置
  _M_start._M_set_node(__nstart);
  _M_finish._M_set_node(__nfinish - 1);
  _M_start._M_cur = _M_start._M_first;
  _M_finish._M_cur = _M_finish._M_first +
               __num_elements % __deque_buf_size(sizeof(_Tp));
}

erase(iterator __pos)

删除指定位置的元素。该函数的有趣之处在于，先判断距离哪一端更近，从近的一侧去移动元素。

insert底层函数insert_aux函数亦然

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
iterator erase(iterator __pos) {
  iterator __next = __pos;
  ++__next;
  difference_type __index = __pos - _M_start; 	//与头距离
  if (size_type(__index) < (this->size() >> 1)) {		//距离与总元素个数比较
    copy_backward(_M_start, __pos, __next);	
      //离头近，将头~pos元素整体向后赋值（覆盖pos），再弹出头
    pop_front();
  }
  else {
    copy(__next, _M_finish, __pos);
      //离尾部近，
    pop_back();
  }
  return _M_start + __index;
}

_M_reserve_map_at_back()

共有两组函数：

  • _M_reserve_map_at_back()和_M_reserve_map_at_front()。表示map的一端不够用时，扩充
  • _M_reserve_element_at_back()和_M_reserve_element_at_front()表示结点不够用扩充结点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
  void _M_reserve_map_at_back (size_type __nodes_to_add = 1) {
    if (__nodes_to_add + 1 > _M_map_size - (_M_finish._M_node - _M_map))
      _M_reallocate_map(__nodes_to_add, false);
  }//map尾结点可用空间不足，换个更大空间
  void _M_reserve_map_at_front (size_type __nodes_to_add = 1) {
    if (__nodes_to_add > size_type(_M_start._M_node - _M_map))
      _M_reallocate_map(__nodes_to_add, true);
  }//map头结点可用空间不足，换个更大空间

template <class _Tp, class _Alloc>
void deque<_Tp,_Alloc>::_M_reallocate_map(size_type __nodes_to_add,
                                          bool __add_at_front)
{
  size_type __old_num_nodes = _M_finish._M_node - _M_start._M_node + 1;
  size_type __new_num_nodes = __old_num_nodes + __nodes_to_add;

  _Map_pointer __new_nstart;
  if (_M_map_size > 2 * __new_num_nodes) {	//总空间充足（元素偏向一侧）则调整位置
    __new_nstart = _M_map + (_M_map_size - __new_num_nodes) / 2 
                     + (__add_at_front ? __nodes_to_add : 0);
    if (__new_nstart < _M_start._M_node)
      copy(_M_start._M_node, _M_finish._M_node + 1, __new_nstart);
    else
      copy_backward(_M_start._M_node, _M_finish._M_node + 1, 
                    __new_nstart + __old_num_nodes);
  }
  else {	//空间不足 新申请一片空间
    size_type __new_map_size = 
      _M_map_size + max(_M_map_size, __nodes_to_add) + 2;
    _Map_pointer __new_map = _M_allocate_map(__new_map_size);	//配置新空间
    __new_nstart = __new_map + (__new_map_size - __new_num_nodes) / 2
                         + (__add_at_front ? __nodes_to_add : 0);	//寻找新头
    copy(_M_start._M_node, _M_finish._M_node + 1, __new_nstart);
    _M_deallocate_map(_M_map, _M_map_size);

    _M_map = __new_map;
    _M_map_size = __new_map_size;
  }

  _M_start._M_set_node(__new_nstart);
  _M_finish._M_set_node(__new_nstart + __old_num_nodes - 1);
}

_M_insert_aux()

insert函数底层调用_M_insert_aux()其中有两个重载版本的_M_insert_aux存在一些问题（非不能，个人认为传参有些冗余）：

1
2
3
4
5
6
7
8
9
10
11
12
13
void deque<_Tp,_Alloc>::_M_insert_aux(iterator __pos,
                                      const value_type* __first,
                                      const value_type* __last,
                                      size_type __n){
    ......
}
template <class _Tp, class _Alloc>
void deque<_Tp,_Alloc>::_M_insert_aux(iterator __pos,
                                      const_iterator __first,
                                      const_iterator __last,
                                      size_type __n){
    .......
}

这两个函数上层insert()函数重载时，传入的是三个参数（Where,First,Last）。而在调用底层_M_insert_aux时，添加第四参数n = first - last。（个人认为这里不传，底层去计算亦可）

stack/queue

stack/queue无迭代器

底层容器可以是vector list deque。然后采用Adapter设计模式，改装成stack/queue。默认底层容器deque。做底层容器要求：拥有empty() size() push_back() pop_back()/pop_front() back()/front() operatot==等函数。（改装时，调用底层容器的函数，能够成功调用。）

priority_queue

默认底层容器vector，默认规则max-heap。插入、删除、弹出元素时调用make_heap() push_heap() pop_heap()

heap

heap无迭代器。

heap不提供外部调用接口，仅供priority_queue使用

默认底层容器vector。根节点位于 vector 的头部；

当 heap 中的某个节点位于 vector 的 i处，左子节点位于 2i+1，右子节点位于 2i+2 ；然后调整为 heap。

heap有四个主要函数:push_heap pop_heap make_heap sort_heap

push_heap

push_heap所做的操作是：向根尾部插入一个元素，然后调整到正确的位置。源码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
template <class _RandomAccessIterator, class _Distance, class _Tp>
void 
__push_heap(_RandomAccessIterator __first,
            _Distance __holeIndex, _Distance __topIndex, _Tp __value)
{
  _Distance __parent = (__holeIndex - 1) / 2; // 找到插入节点的父节点位置
  while (__holeIndex > __topIndex && *(__first + __parent) < __value) { // 当插入值大于其父节点的值
    *(__first + __holeIndex) = *(__first + __parent);   // 将其插入节点的父节点的值赋给插入节点位置
    __holeIndex = __parent;  // 索引位置改变，插入值的索引为父节点索引
    __parent = (__holeIndex - 1) / 2; // 插入值的索引的父节点
  }    
  *(__first + __holeIndex) = __value; // 交换完后，找到插入值的真正位置，赋值
}

  • __first — 容器首部迭代器，用于定位元素的位置(下面的*(__first + __holeIndex))

  • __holeIndex — 容器已使用的长度、也是新插入元素在数组中存放的角标

  • __topIndex — 允许上升的最大高度，用于控制循环退出条件(一般为根节点高度0)

  • __value — 新插入元素的值

  • __comp — 仿函数，用于传入自定义比较规则。（影响上述源码第7行循环中的比较标准）

    • *(__first + __parent) < __value) ⟶__comp(*(__first + __parent), __value))

pop_heap

pop_heap调用__pop_heap实现弹堆顶元素。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
template <class _RandomAccessIterator>
inline void pop_heap(_RandomAccessIterator __first,_RandomAccessIterator __last){
  __pop_heap_aux(__first, __last, __VALUE_TYPE(__first));   // pop_heap 调整函数，将 vector 头部元素放到 vector 的尾部
}
template <class _RandomAccessIterator, class _Tp>
inline void __pop_heap_aux(_RandomAccessIterator __first, _RandomAccessIterator __last,_Tp*){
  __pop_heap(__first, __last - 1, __last - 1, _Tp(*(__last - 1)), __DISTANCE_TYPE(__first)); 
    // 调整 heap 后，变为[first, last-1)
    //这里还要注意，第四个参数__value传的是_Tp(*(__last - 1))。也就是原来堆尾的值。
}
template <class _RandomAccessIterator, class _Tp, class _Distance>
inline void __pop_heap(_RandomAccessIterator __first, _RandomAccessIterator __last,
           _RandomAccessIterator __result, _Tp __value, _Distance*)
{
  *__result = *__first;  // 先保存 vector 头部元素，放到 vector 的尾端
  __adjust_heap(__first, _Distance(0), _Distance(__last - __first), __value); // 再做 shift down 操作调整
}

__pop_heap参数如下

  • __first — 指向堆顶的迭代器。（要弹出元素的位置）

  • __last — 容器尾部迭代器（实际使用的最后一个元素位置）

  • __result — 结果保存的位置。由于底层容器为vector，当删除一个元素时，是将其移动到容器尾，然后再移动尾迭代器使其不可见，故默认值为_Tp(*__last )

  • __value — 堆中最小的元素值（堆尾部的值）

  • __comp — 仿函数，用于传入自定义比较规则。如果有会相应的传给__adjust_heap函数

__adjust_heap

pop_heap底层真正调用实现剩余元素维持堆序性的函数。这里以删除结点后的调整为例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
template <class _RandomAccessIterator, class _Distance, class _Tp>
void 
__adjust_heap(_RandomAccessIterator __first, _Distance __holeIndex,
              _Distance __len, _Tp __value)
{
  _Distance __topIndex = __holeIndex;  // __holeIndex = 0，为 heap 的根节点
  _Distance __secondChild = 2 * __holeIndex + 2; // 根节点的右节点的索引
  while (__secondChild < __len) {
      // __comp	传入时，用来修改此处的比较条件
    if (*(__first + __secondChild) < *(__first + (__secondChild - 1))) // 比较根节点的左右节点值
      __secondChild--;//__secondChild向下传递时，一定为较大值
    *(__first + __holeIndex) = *(__first + __secondChild);  // while 里做 shift down 操作
      //二者本来是兄弟节点，较大值升为父节点。
    __holeIndex = __secondChild;
    __secondChild = 2 * (__secondChild + 1);
  }
  if (__secondChild == __len) {  // 没有右子节点，只有左子节点
    *(__first + __holeIndex) = *(__first + (__secondChild - 1));
    __holeIndex = __secondChild - 1;
  }
   //循环退出时，__holeIndex移动到最后一层。
    // 此时。__holeIndex标志着最小值__value的位置
  __push_heap(__first, __holeIndex, __topIndex, __value);  // 向上寻找 找到真正的位置，插入
}

抛开删除元素移动最小值而言，当我们所操作的是任意一个元素时，所进行的操作是先将其下降到最深深度，然后将其上升至适当位置，但是最终这个位置不能大于其原本的位置。

make_heap

递归调用__adjust_heap()进行调整 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// [first, last) 调整为 heap
template <class _RandomAccessIterator, class _Tp, class _Distance>
void 
__make_heap(_RandomAccessIterator __first,
            _RandomAccessIterator __last, _Tp*, _Distance*)
{
  if (__last - __first < 2) return; // 如果长度为 0 或 1，不排列
  _Distance __len = __last - __first; // 待排列的长度
  _Distance __parent = (__len - 2)/2; // 父节点i和右子节点2i+2
    
  while (true) { // 这里 __parent 就是待插入节点索引
    __adjust_heap(__first, __parent, __len, _Tp(*(__first + __parent)));
    if (__parent == 0) return;
    __parent--;
  }
}

sort_heap

重复调用pop_heap函数，将当前最大值丢到尾部。

1
2
3
4
5
6
7
8
9
template <class _RandomAccessIterator, class _Compare>
void 
sort_heap(_RandomAccessIterator __first,
          _RandomAccessIterator __last, _Compare __comp)
{
  __STL_REQUIRES(_RandomAccessIterator, _Mutable_RandomAccessIterator);
  while (__last - __first > 1)
    pop_heap(__first, __last--, __comp);
}

既然sort_heap已经可以实现排序，那make_heap作用？

首先，我们在priority_queue底层了解到其存在如下构造函数。

1
2
priority_queue(const value_type* __first, const value_type* __last) 
    : c(__first, __last) { make_heap(c.begin(), c.end(), comp); }

当我们为其传入一个vector的首尾指针时（测试list亦可），会先把相应的值赋给底层容器里，然后调用make_heap函数，将拷贝到底层容器里的值进行排序。

后话：暂时在该版本源码中并未发现sort_heap的调用

关联式容器

RB-Tree

红黑树，是一个自平衡的二叉搜索树。

首先用bool类型定义结点的红黑色。

1
2
3
typedef bool _Rb_tree_Color_type;
const _Rb_tree_Color_type _S_rb_tree_red = false; // 红色为 0
const _Rb_tree_Color_type _S_rb_tree_black = true; // 黑色为 1

红黑树的虚拟头结点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
template <class _Tp, class _Alloc>
struct _Rb_tree_base
{
protected:
    _Rb_tree_node<_Tp>* _M_header;
};

class _Rb_tree : protected _Rb_tree_base<_Value, _Alloc> {
protected:
    size_type _M_node_count; // keeps track of size of tree 节点数量
    _Compare _M_key_compare; // 节点间的键值大小比较准则
};
_Link_type& _M_root() const 
{ return (_Link_type&) _M_header->_M_parent; }
_Link_type& _M_leftmost() const 
{ return (_Link_type&) _M_header->_M_left; }
_Link_type& _M_rightmost() const 
{ return (_Link_type&) _M_header->_M_right; }
  • 对于一个空树而言。
    • header的left right指针指向自己
    • header->parent = nullptr
  • 红黑树非空
    • root->parent = header && header->parent = root
    • header->left = leftmost(最小值结点) && header->right = rightmost(最大值结点)

node

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
struct _Rb_tree_node_base
{
  typedef _Rb_tree_Color_type _Color_type;
  typedef _Rb_tree_node_base* _Base_ptr;
  _Color_type _M_color;   // 节点颜色，非红即黑
  _Base_ptr _M_parent;    // 父节点
  _Base_ptr _M_left;      // 左节点
  _Base_ptr _M_right;     // 右节点
    //此外，还有找最大值、最小值的函数，二叉搜索树最大值、最小值即为最右侧、最左侧结点。
};
template <class _Value>
struct _Rb_tree_node : public _Rb_tree_node_base
{
  typedef _Rb_tree_node<_Value>* _Link_type;
  _Value _M_value_field;  // 节点值
};

iterator

1
2
3
4
5
6
// RB-tree 的迭代器-基类
struct _Rb_tree_base_iterator
{
  typedef _Rb_tree_node_base::_Base_ptr _Base_ptr;
  _Base_ptr _M_node; // 它用来与容器之间产生一个连接关系
};

decrement/increment

迭代器++/--的底层，用于寻找前驱、后继节点（按值的大小序），但其中对虚拟header结点有着特殊处理。最左值的前一个和最右值的后一个结点均为header

end()

返回最右值的后一个元素(header)

equal_range

1
2
3
4
5
6
7
template <class _Key, class _Value, class _KeyOfValue,  class _Compare, class _Alloc>
inline pair<typename _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>::iterator,
     		typename _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>::iterator>
_Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>::equal_range(const _Key& __k)
{
  return pair<iterator, iterator>(lower_bound(__k), upper_bound(__k));
}// key == _k的结点迭代器所在的范围。

  • lower_bound(const _Key& __k) — 不小于k的第一个节点的迭代器

  • upper_bound(const _Key& __k) — 大于k的第一个节点的迭代器

__rb_verify()

判断红黑树是否合法。（满足红黑树的性质）

源码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
template <class _Key, class _Value, class _KeyOfValue,  class _Compare, class _Alloc>
bool _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>::__rb_verify() const
{
    if (_M_node_count == 0 || begin() == end())
        return _M_node_count == 0 && begin() == end() &&
        _M_header->_M_left == _M_header && _M_header->_M_right == _M_header;
  //true代表此空树符合红黑树的性质
    int __len = __black_count(_M_leftmost(), _M_root());	//每个分支上黑节点个数
    for (const_iterator __it = begin(); __it != end(); ++__it) {
        _Link_type __x = (_Link_type) __it._M_node;
        _Link_type __L = _S_left(__x);
        _Link_type __R = _S_right(__x);

     //红黑树性质之 红节点的子节点均为黑
        if (__x->_M_color == _S_rb_tree_red)
            if ((__L && __L->_M_color == _S_rb_tree_red) ||
                (__R && __R->_M_color == _S_rb_tree_red))
                return false;
      //二叉搜素树结点间大小关系
        if (__L && _M_key_compare(_S_key(__x), _S_key(__L)))
            return false;
        if (__R && _M_key_compare(_S_key(__R), _S_key(__x)))
            return false;
	//统计一条分支上黑节点个数 与基准值不同  则不符合
        if (!__L && !__R && __black_count(__x, _M_root()) != __len)
            return false;
    }
//左节点不是最小值、右节点不是最大值
    if (_M_leftmost() != _Rb_tree_node_base::_S_minimum(_M_root()))
        return false;
    if (_M_rightmost() != _Rb_tree_node_base::_S_maximum(_M_root()))
        return false;

    return true;
}

set/multiset

底层容器为红黑树。函数实现为调用红黑树相应的函数。两个的区别在于insert函数

  • set调用红黑树的insert_unique函数
  • multiset调用红黑树的insert_equal函数
1
2
3
4
5
6
7
8
9
10
template <class _Key, class _Compare, class _Alloc>
class set{
    typedef _Key     key_type;
    typedef _Key     value_type;
    typedef _Compare key_compare;
    typedef _Compare value_compare;
    typedef _Rb_tree<key_type, value_type, _Identity<value_type>, key_compare, _Alloc> _Rep_type;
    // set 的底层实现为 RB-tree
    _Rep_type _M_t;  // red-black tree representing set
};

map/multimap

除了下述基础结构和set/mutiset有细微差距外，整体与set/mutiset类似、

1
2
3
4
5
6
7
8
9
10
11
12
template <class _Key, class _Tp, class _Compare, class _Alloc>
class map {
    typedef _Key                  key_type; // 键值类型
    typedef _Tp                   data_type; // 实值类型
    typedef _Tp                   mapped_type;
    typedef pair<const _Key, _Tp> value_type;  // 元素类型(键值/实值)
    typedef _Compare              key_compare; // 键值比较函数
    _Compare comp;
    typedef _Rb_tree<key_type, value_type,  _Select1st<value_type>, key_compare, _Alloc> _Rep_type; 
    // map 的底层机制 RB-tree 
    _Rep_type _M_t;  // red-black tree representing map 以红黑树(RB-tree) 表现 map
};

pair

map 的结构是键值对 <Key, value>，这种结构在底层以pair形式存储。基本结构如下：

1
2
3
4
5
6
7
template <class _T1, class _T2>
struct pair {
    typedef _T1 first_type;
    typedef _T2 second_type;
    _T1 first;  // 第一个参数
    _T2 second; // 第二个参数
};

opertor<

先比较第一参数大小关系，第一参数相等时，再比较第二参数。

1
2
3
4
5
template <class _T1, class _T2>
inline bool operator<(const pair<_T1, _T2>& __x, const pair<_T1, _T2>& __y)
{ 
    return __x.first < __y.first || (!(__y.first < __x.first) && __x.second < __y.second); 
}

make_pair

1
2
3
4
5
template <class _T1, class _T2>
inline pair<_T1, _T2> make_pair(const _T1& __x, const _T2& __y)
{
    return pair<_T1, _T2>(__x, __y);
}

bitset

整体实现上与bit_vector有些类似。

1
2
3
4
5
6
template<size_t _Nw>	//使用时传入的bitset中的位数
struct _Base_bitset {
    typedef unsigned long _WordT;

    _WordT _M_w[_Nw];
}:

__BITSET_WORDS

当我们声明一个bitset时，该宏定义用于计算出需要多少个unsigned int才能存储这些bit

1
#define __BITSET_WORDS(__n) ((__n) < 1 ? 1 : ((__n) + __BITS_PER_WORD - 1)/__BITS_PER_WORD)

由于操作系统位数不同，可能会带来歧义。该模块用于自动推导出unsigned int所占空间大小。

1
#define __BITS_PER_WORD (CHAR_BIT*sizeof(unsigned long))

_Bit_count

该数组提供一个对照表用于判断角标所代表元素的二进制标志中1的个数。

如 7=111(2),故_Bit_count[7] = 3

1
2
3
4
template<bool __dummy> 
struct _Bit_count {
    static unsigned char _S_bit_count[256];
};

_First_one

1
2
3
4
template<bool __dummy> 
struct _First_one {
    static unsigned char _S_first_one[256];
};

同样的，该数组也起到对照作用。该数组表示首个1开始，后面二进制值为0的个数。

如 7=111(2),故_First_one[7] = 0

_S_whichword

获取比特位__pos在数组中的下标。

1
2
static size_t _S_whichword( size_t __pos )
	{ return __pos / __BITS_PER_WORD; }

_S_whichbyte

获取在word中第几个char

1
2
static size_t _S_whichbyte( size_t __pos )
	{ return (__pos % __BITS_PER_WORD) / CHAR_BIT; }

_S_whichbit

获取在word中第几个bit

1
2
static size_t _S_whichbit( size_t __pos )
        { return __pos % __BITS_PER_WORD; }

_S_maskbit

1
2
3
typedef unsigned long _WordT;
static _WordT _S_maskbit( size_t __pos )
    { return (static_cast<_WordT>(1)) << _S_whichbit(__pos); }

移位，以供set reset flip等调用

为实现一些功能，封装了一些简单函数

函数 含义 调用
_M_do_and() bitset之间逻辑与 & &=
_M_do_or() bitset之间逻辑或 | |=
_M_do_xor() bitset之间逻辑异或 ^ ^=
_M_do_flip() 逐元素取反 flip() ~
_M_do_left_shift() 左移 << <<=
_M_do_right_shift() 右移 >> >>=
_M_do_set() 置为1 set()
_M_do_reset() 置为0 reset()
_M_is_equal() 判断是否相等 == !=
_M_is_any() 是否有值为1的位 any() none()
_M_do_count() 值为1的位的个数 count()
_M_do_to_ulong() 01串转换成整数 to_ulong()
_M_copy_to_string() 赋值给string to_string()

重载cin/cout

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
template <size_t _Nb>
istream& operator>>(istream& __is, bitset<_Nb>& __x) {
    string __tmp;
    __tmp.reserve(_Nb);

    if (__is.flags() & ios::skipws) {
        char __c;
        do 
            __is.get(__c);
        while (__is && isspace(__c));
        if (__is)
            __is.putback(__c);
    }

    for (size_t __i = 0; __i < _Nb; ++__i) {
        char __c;
        __is.get(__c);

        if (!__is)
            break;
        else if (__c != '0' && __c != '1') {
            __is.putback(__c);
            break;
        }
        else
            __tmp.push_back(__c);
    }

    if (__tmp.empty()) 
        __is.clear(__is.rdstate() | ios::failbit);
    else
        __x._M_copy_from_string(__tmp, static_cast<size_t>(0), _Nb);

    return __is;
}
//输出 以字符串形式输出
template <size_t _Nb>
ostream& operator<<(ostream& __os, const bitset<_Nb>& __x) {
    string __tmp;
    __x._M_copy_to_string(__tmp);
    return __os << __tmp;
}

hashtable

哈希表的链式避免冲突法在成链时，新插入的元素在头部。（头插）

结点

1
2
3
4
5
6
template <class _Val>
struct _Hashtable_node
{
  _Hashtable_node* _M_next;	//用于链式连接
  _Val _M_val;
};

迭代器

1
2
3
4
5
6
7
8
9
10
11
template <class _Val, class _Key, class _HashFcn,
          class _ExtractKey, class _EqualKey, class _Alloc>
struct _Hashtable_iterator {
    typedef hashtable<_Val,_Key,_HashFcn,_ExtractKey,_EqualKey,_Alloc> _Hashtable;
    typedef _Hashtable_node<_Val> _Node; // hash table 节点
    typedef forward_iterator_tag iterator_category; // 迭代器类型：前向迭代器

    _Node* _M_cur; // 迭代器目前所指的节点
    _Hashtable* _M_ht; // 保持对容器的连接关系，bucket
    ...
};

bucket

一共提供28个bucket大小。设置的原则为，2倍扩充附近的质数。分别如下:

1
2
3
4
5
6
7
8
9
10
enum { __stl_num_primes = 28 };
static const unsigned long __stl_prime_list[__stl_num_primes] =
{
  53ul,         97ul,         193ul,       389ul,       769ul,
  1543ul,       3079ul,       6151ul,      12289ul,     24593ul,
  49157ul,      98317ul,      196613ul,    393241ul,    786433ul,
  1572869ul,    3145739ul,    6291469ul,   12582917ul,  25165843ul,
  50331653ul,   100663319ul,  201326611ul, 402653189ul, 805306457ul, 
  1610612741ul, 3221225473ul, 4294967291ul
};

hashtable

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
template <class _Val, class _Key, class _HashFcn,
          class _ExtractKey, class _EqualKey, class _Alloc>
class hashtable {
public:
    typedef _Key key_type; // 节点的键值
    typedef _Val value_type; // 节点的实值
    typedef _HashFcn hasher; // 哈希函数
    typedef _EqualKey key_equal; // 判断键值是否相同
private:
    typedef _Hashtable_node<_Val> _Node; // 节点
    hasher                _M_hash;
    key_equal             _M_equals;
    _ExtractKey           _M_get_key;
    vector<_Node*,_Alloc> _M_buckets; // vector 容器
    size_type             _M_num_elements;
};

  • _Val — 节点的实值类型

  • _Key — 节点的键值类型

  • _HashFcn — 哈希函数的类型

  • _ExtractKey — 从节点中取出键值的方法

  • _EqualKey — 判断键值是否相同的方法

  • _Alloc — 空间配置器

bkt_num

我们知道可以通过Key来获取到元素相应的bucket、重复的个数等信息。利用该函数，可以通过Value获取到相应信息。

1
2
3
4
5
6
7
8
9
size_type _M_bkt_num(const value_type& __obj) const
{
    return _M_bkt_num_key(_M_get_key(__obj));
}
size_type _M_bkt_num(const value_type& __obj, size_t __n) const
{
    return _M_bkt_num_key(_M_get_key(__obj), __n);
}
//向上寻定义	_ExtractKey           _M_get_key;

__stl_hash_string

各种数字(int、unsigned int、long、unsigned long、short)以及字符char进行传入的是原值、除此之外字符串类型(char*)会进行转换:

1
2
3
4
5
6
7
8
inline size_t __stl_hash_string(const char* __s)
{
    unsigned long __h = 0; 
    for ( ; *__s; ++__s)
        __h = 5*__h + *__s;

    return size_t(__h);
}

hashmap/hashset

hash_set/hash_map 底层实现机制是 hash table，所以 hash_set/hash_map 内部实现就是封装hashtable类。与map/set和multimap/multiset基于红黑树改装类似，再次不过多赘述。

-------------感谢阅读有缘再见-------------